IBM e il quantum computing per tutti
Due anni fa è avvenuto, un po’ in sordina, uno di quegli eventi che potrà avere ripercussioni a lungo termine sullo sviluppo dell’informatica: IBM ha aperto l’accesso, tramite cloud computing, al proprio calcolatore quantistico. Si tratta di qualcosa di cui tutti, anche i meno esperti, hanno sentito parlare, ma spesso si fa molta confusione sull’argomento e non si riescono a comprendere appieno le implicazioni di questa rivoluzione. Naturalmente, per capirle dobbiamo prima capire la differenza tra un computer classico ed uno quantistico. Prima di cominciare, però, specifichiamo un punto importante: la rivoluzione non è ancora iniziata, la si sta soltanto preparando, per ora. Con l’attuale computer quantistico di IBM non si può fare molto, e le normali operazioni di programmazione sembrano inutilmente complicate. Questo perché la potenza di calcolo è ancora troppo bassa. Naturalmente, il problema dei computer quantistici è che man mano che la loro potenza (o, se volete, il numero di qubit, lo spiegheremo più avanti) aumenta diventano molto più difficili e costosi da costruire. Ed è per questo motivo che IBM permette l’accesso a tutti i programmatori tramite il cloud: in questo modo potrà contare su una squadra di alfa-tester volontari, e potrà cercare di migliorare l’efficienza del calcolatore scoprendo i problemi che salteranno fuori durante i vari test. Insomma, i calcolatori quantistici per ora non sono utili. Ma tra qualche anno potrebbero esplodere con la loro potenza, e potrebbero consentirci di eseguire algoritmi che oggi con un computer classico non si possono proprio realizzare.
Le macchine di Turing
Un computer è fondamentalmente una macchina di Turing. Una macchina di Turing è un modello matematico che rappresenta ciò che un calcolatore programmabile può fare. Ovviamente, ciò che un calcolatore può fare nel mondo reale è dettato dalle leggi della fisica classica. La macchina di Turing nasce per rispondere ad una domanda: esiste sempre un metodo attraverso cui un qualsiasi enunciato matematico possa essere stabilito come vero o falso? In altre parole, è possibile sviluppare un algoritmo con cui capire se una qualunque affermazione sia vera o falsa?
La risposta è no, non è possibile sviluppare un algoritmo generale che stabilisca la veridicità di una qualsiasi affermazione, e questo perché in realtà il concetto di “algoritmo” non è ben definito. Tuttavia, Alan Turing propose comunque un modello matematico (la sua famosa “macchina”) con cui verificare, per ogni singola affermazione, se sia possibile arrivare a stabilirla come vera o falsa. Con una macchina di Turing infatti è possibile sviluppare algoritmi per ridurre una affermazione ai suoi componenti di base, cercando di verificarla, e vi sono due opzioni: o la macchina ad un certo punto termina l’algoritmo e fornisce una risposta, oppure l’algoritmo andrà avanti all’infinito (in una sorta di loop continuo, chiamato halting) senza mai fornire una risposta. Oggi si usa proprio la macchina di Turing per definire il concetto di “algoritmo”.
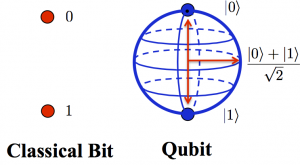
Mentre un bit ha due soli possibili valori, un qubit ha una probabilità di essere più vicino a 1 o a 0, quindi è un qualsiasi numero compreso tra 0 e 1
Una macchina di Turing utilizza come input-output un nastro su cui legge e scrive un valore alla volta, in una precisa cella del nastro, ed in ogni istante di tempo t(n) la macchina avrà un preciso stato s(n) che è il risultato dell’elaborazione. Ovviamente la macchina può eseguire alcune operazioni fondamentali: spostarsi di una cella avanti, spostarsi di una cella indietro, scrivere un simbolo nella casella attuale, cancellare il simbolo presente nella casella attuale, e fermarsi.
Un modello così rigido, che esegue operazioni elementari per tutto il tempo che si ritiene necessario, può di fatto svolgere qualsiasi tipo di calcolo concepibile. Tuttavia, così come Godel aveva dimostrato che alcuni teoremi non si possono dimostrare senza cadere in un ciclo infinito, anche con la macchina di Turing non è detto che arrivi ad un risultato, perché alcuni calcoli non si possono portare a termine senza cadere in un processo infinito (in altre parole, il tempo necessario per la soluzione sarebbe infinito, e nel mondo reale nessuno di noi può aspettare fino all’infinito per avere una risposta). Per fare un esempio banale, se ciò che vogliamo fare è semplicemente ottenere il risultato di 3*4, è ovvio che basta scomporre il problema nei suoi termini fondamentali, ovvero un ciclo ripetuto 4 volte in cui si somma +3. Il ciclo richiede un numero finito di passaggi, quindi la moltiplicazione 3*4 è una operazione che può essere svolta con una macchina di Turing senza cadere nell’halting. Se volessimo moltiplicare due numeri enormi servirebbe un ciclo con molti più passaggi, ma sarebbero comunque un numero finito, quindi anche se potrebbe essere necessario un tempo molto lungo, prima o poi il ciclo finirebbe e la macchina produrrebbe un risultato.
Dalla fisica classica alla fisica quantistica
Ora, abbiamo detto che per la macchina di Turing valgono le leggi della fisica classica, e ci riferiamo in particolare ai principi della termodinamica. Il primo principio stabilisce quali eventi siano possibili e quali no, il secondo principio stabilisce quali eventi siano probabili e quali no. Il primo principio, espresso come definizione dell’energia interna di un sistema (U):
dU=Q-L
ci dice che l’energia interna di un sistema chiuso non si crea e non si distrugge, ma si trasforma ed il suo valore rimane dunque costante. Infatti, in un sistema isolato Q=0 (il calore) quindi dU=-L, ovvero l’energia interna può trasformarsi in lavoro e viceversa senza però sparire magicamente. Il secondo principio, che viene espresso con l’equazione
dS/dt>=0
ci dice che ogni evento si muove sempre nella direzione che fa aumentare l’entropia e mai nell’altra. Al massimo può rimanere costante, nelle rare situazioni reversibili. Infatti la derivata dell’entropia (S) in funzione del tempo (t) è sempre maggiore o uguale a zero. In altre parole, l’enunciato del secondo principio della termodinamica si può riassumere con la frase “riscaldando un acquario si ottiene una zuppa di pesce, ma raffreddando una zuppa di pesce non si ottiene un acquario”. Insomma, la maggioranza degli eventi termodinamici non è reversibile, almeno nel mondo reale, e questo vale anche per la macchina di Turing.
Una macchina di Turing quantistica, invece, si baserebbe sulle leggi fisiche della meccanica quantistica, e quindi le sue operazioni potrebbero essere reversibili. Il vantaggio ovvio è che se le operazioni sono reversibili di fatto non è possibile che la macchina quantistica cada nell’halting della macchine di Turing classiche. Basandosi proprio sulla meccanica quantistica, ci saranno una serie di differenze con la macchina di Turing classica:
- un bit quantistico, chiamato qubit, non può essere letto con assoluta precisione. In genere, si fa soltanto una previsione probabilistica del fatto che sia più vicino a 0 o a 1
- la lettura di un qubit è una operazione che lo danneggia modificandone lo stato, quindi non è più possibile leggerlo nuovamente
- date le due affermazioni precedenti, è ovvio che non si possano conoscere con precisione le condizioni iniziali e nemmeno i risultati
- un qubit può essere spostato da un punto all’altro con precisione assoluta, a condizione che l’originale venga distrutto: è il teletrasporto quantistico
- i qubit non possono essere scritti direttamente, ma si possono scrivere sfruttando l’entanglement, cioè la correlazione quantistica
- un qubit può essere 0 od 1, ma può anche essere una combinazione di questi due stati (un po’ 0, un po’ 1, come il gatto di Schroedinger), quindi può di fatto contenere molte più informazioni di un normale bit
Apparentemente, queste caratteristiche rendono la macchina inutile, ma è solo il punto di vista di una persona abituata a ragionare nel modo tradizionale. In realtà, una macchina di Turing quantistica è imprecisa durante il momento di input e quello di output, ma è infinitamente precisa durante i passaggi intermedi.
Per chi non ha studiato le basi della fisica, uno sviluppatore ha scritto una guida che riassume alcuni dei concetti fondamentali, soprattutto per quanto riguarda le porte logiche, fondamentali per manipolare i qubit.
I qubit possono essere implementati misurando la proprietà di spin dei nuclei degli atomi di alcune molecole, oppure la polarizzazione dei fotoni (anche i fotografi dilettanti sanno che la luce, composta da fotoni, può essere polarizzata usando appositi filtri). In realtà, pensandoci bene, ci si può accorgere che una macchina di Turing quantistica non è altro che una macchina di Turing il cui nastro di lettura/scrittura contiene valori casuali. Qual è il vantaggio della casualità? Semplice: la possibilità di fare tentativi a caso per cercare la soluzione di un problema che non si riesce ad affrontare con un algoritmo tradizionale. Naturalmente, aiutando un po’ il caso con un algoritmo.
Il vantaggio della casualità “vera”
Nei casi degli algoritmi più semplici, questa idea è solo una complicazione, ma in algoritmi molto complessi e lenti la macchina quantistica può fornire un risultato accettabile in tempi molto ridotti. Possiamo fare un paragone con il metodo Monte Carlo, un metodo per ottenere un risultato approssimato sfruttando tentativi casuali. Facciamo un esempio: immaginiamo di avere una sagoma disegnata su un muro e di voler misurare la sua area. Se la sagoma è regolare, come un cerchio, è facile: basta usare l’apposito algoritmo (per esempio “raggio al quadrato per pi greco”). Ma se la sagoma è molto più complicata, come la silhouette di un albero, sviluppare un apposito algoritmo diventa estremamente complicato e lento. Il metodo Monte Carlo ci suggerisce di prendere un fucile mitragliatore e cominciare a sparare a caso contro il muro: dopo un po’ di tempo non dovremo fare altro che contare il numero di proiettili che sono finiti dentro alla sagoma e moltiplicare tale numero per la superficie di un singolo proiettile (facile da calcolare sulla base del calibro). Otterremo una buona approssimazione della superficie della sagoma: la qualità dell’approssimazione dipende dal numero di proiettili abbiamo sparato col fucile ma, comunque vada, il tempo complessivo per ottenere il valore della superficie è decisamente poco rispetto all’uso di un algoritmo metodico. Un metodo simile che si usa molto nell’informatica moderna è rappresentato dagli algoritmi genetici, i quali hanno però tre svantaggi: uno è che deve essere possibile sviluppare una funzione di fitness, cosa non sempre possibile (per esempio non si può fare nel brute force di una password), e l’altro è che comunque verrebbero eseguiti su una macchina che si comporta in modo classico, quindi il sistema sarebbe comunque poco efficiente (pur offrendo qualche vantaggio in termini di tempistica). Inoltre, è praticamente impossibile ottenere delle mutazioni davvero casuali nei codici genetici che si utilizzano per cercare una soluzione: nei computer classici la casualità non esiste, è solo una illusione prodotta da qualche algoritmo che a sua volta non è casuale. I qubit risolvono questi problemi, visto che sono rappresentati da oggetti fisici che sono naturalmente casuali.
Scomposizione in fattori primi
Ovviamente, uno degli utilizzi più interessanti di una macchina di Turing quantistica è l’esecuzione di un algoritmo di fattorizzazione di Shor. Come si impara a scuola, fattorizzare un numero (cioè scomporlo nei fattori primi) è una operazione che richiede molto tempo, sempre di più man mano che il numero diventa grande. Si tratta di una cosa molto importante perché l’RSA, la crittografia che al momento protegge qualsiasi tipo di comunicazione (dai messaggi privati alle transazioni finanziarie) si basa proprio sui numeri primi e la sua sicurezza è dovuta al fatto che con un normale computer, ovvero una macchina di Turing classica, scomporre in fattori primi un numero sia una operazione talmente lenta che sarebbero necessari degli anni per riuscirci. Ma sfruttando un calcolatore quantistico e l’algoritmo di fattorizzazione di Shor, questa operazione diventa “facile” e la si può svolgere in un tempo che si calcola con un polinomio, dunque è un tempo “finito” invece di “infinito” e solitamente abbastanza breve. Con questo algoritmo, si potrebbero calcolare le chiavi private di cifratura di tutti i messaggi più riservati, e l’intera sicurezza delle telecomunicazioni crollerebbe. Al momento, con gli attuali computer quantistici, non è possibile applicare l’algoritmo di Shor in modo generale, ma sono già state realizzate alcuni versioni semplificate dell’algoritmo adattate per specifici casi. Se i computer quantistici diventassero più potenti ed affidabili, diventerebbe possibile sfruttare l’algoritmo su qualsiasi chiave crittografica e far crollare la sicurezza di internet. Il mondo, comunque, non tornerebbe all’età della pietra: sempre usando i computer quantistici sarebbe possibile utilizzare un sistema di crittografia a “blocco monouso” con distribuzione quantistica della chiave crittografica, l’unico metodo di cifratura che sarebbe davvero inviolabile. Nel senso che affinché si possa forzare la crittografia con chiave quantistica le leggi della fisica dovrebbero essere sbagliate (e non lo sono).
Il quantum computer IBM è gratuito?
Al momento in cui scriviamo, l’accesso al calcolatore quantistico di IBM è gratuito. Quando ci si registra, si ottengono una decina di “units”, cioè dei crediti virtuali. L’esecuzione di un programma costa intorno alle 3 units. Quando le proprie units sono terminate, dopo 24 ore IBM ricarica automaticamente le units iniziali, così si può continuare a sperimentare.
Un esempio pratico: OpenQASM
Il computer quantistico di IBM ha 5 qubit, ma per la maggioranza degli algoritmi sviluppati finora se ne usano soltanto due. Una operazione che può essere interessante provare è la trasformata di Fourier: per chi non la conoscesse, si tratta di una trasformazione che permette di “semplificare” una funzione algebrica riducendone il rumore e rimuovendo i dati non interessanti. Siccome la sua implementazione in un calcolatore classico può essere lunga, è stato sviluppato un algoritmo chiamato FFT, cioè trasformata di Fourier veloce. Per implementare una trasformata di Fourier nel computer quantistico IBM si usa il suo linguaggio nativo OpenQASM:
La sintassi del linguaggio è una via di mezzo tra assembly e C: qreg crea un registro di bit quantistici (4, nell’esempio) mentre creg crea un registro di bit classici (sempre 4). Poi si possono applicare dei gate, ovvero delle porte logiche ai qubit. Per esempio, applicando il gate X ai qubit 0 e 2, il registro q diventerà 1010, perché questa porta logica non fa altro che invertire il valore di un qubit (che di default è sempre 0). Il comando barrier impedisce che avvengano trasformazioni nei qubit. Altri tipi di porte logiche sono H e CU1. La prima serve a produrre una variazione casuale nella probabilità di un qubit, cioè nella probabilità che esso sia più vicino ad essere 0 oppure 1. Eseguendo il gate H su tutti i qubit, ci si assicura che i loro stati siano davvero casuali. La seconda, invece, è una delle porte logiche fornite da IBM (ce ne sono una dozzina), che permette di eseguire i passaggi per la serie di Fourier. Infine, il comando measure traduce i qubit in bit riempiendo il registro classico c, i cui valori possono quindi essere letti senza problemi.
Sul sito https://quantumexperience.ng.bluemix.net/ è possibile iscriversi usando il proprio account GitHub o Google
Naturalmente, grazie alla casualità, se si esegue l’algoritmo più volte si otterranno risultati diversi. Tuttavia, con questo algoritmo si può approssimare in un tempo molto breve una trasformata di Fourier per l’array classico 1010. Ovviamente, non si può davvero utilizzare questo algoritmo per analizzare il segnale di un ricevitore radio, non sarebbe affatto pratico. Però in futuro potremmo riuscire ad avere computer quantistici tanto potenti da permetterci di eseguire una trasformata di Fourier, approssimata, in tempi rapidi anche per quantità di dati enormi. Intanto, possiamo provare a giocarci un po’ e a inventare nuovi gate, nuove porte logiche per i qubit. In fondo, il motivo per cui IBM ha reso pubblico l’accesso al calcolatore quantistico è che soltanto sperimentando nuovi utilizzi di questo tipo di computer sarà possibile aumentare l’efficienza e soprattutto capire quanto davvero il qubit rivoluzionerà la storia dell’informatica e la vita di tutti i giorni.
Caricare codice QASM con Python
Per caricare un programma sul cloud di IBM ed eseguirlo con il processore quantistico si può installare l’apposita libreria direttamente con il comando:
Poi si può sfruttare il codice di test per provare il caricamento di un codice OpenQASM. Prima di tutto si deve modificare il file config.py inserendo il proprio token di autorizzazione personale:
e poi si può avviare il programma. Il suo codice è abbastanza semplice, ne presentiamo i punti salienti:
Il programma comincia importando la libreria di IBM ed il file config che contiene il token.
Le varie funzione del programma sono inserite in una apposita classe, chiamata TestQX, per sfruttare la programmazione ad oggetti dalla routine principale.
Una delle prime funzioni è quella che si occupa della verifica del token: viene creato l’oggetto api, dal quale si possono ottenere le credenziali utilizzando con il metodo _check_credentials(). La funzione restituisce un valore true se le credenziali sono valide.
Un’altra funzione, sfruttando il metodo get_last_codes() permette di verificare se siano già stati caricati dei codici con il proprio token, in modo da poterli eventualmente avviare o poter controllare i risultati. Questa funzione, però, può essere utile più che altro in un utilizzo meno sperimentale di quello che faremo le prime volte che proviamo il calcolatore quantistico.
La funzione test_api_run_experiment esemplifica l’esecuzione di un codice OpenQASM sul computer quantistico. Oltre a costruirsi un oggetto per accedere alle API, si deve inserire tutto il codice OpenQASM all’interno di una variabile. Potremmo leggere il codice da un file di testo, ma ovviamente per un semplice test conviene scrivere tutto il codice direttamente nel programma. Ovviamente tutto il codice QASM può essere scritto su una sola riga perché le varie righe possono essere separate con un punto virgola (come nel linguaggio C).
Una opzione da definire è il device: può essere di due tipi, simulator oppure real, a seconda del fatto che il codice debba essere eseguito su un simulatore oppure sul vero calcolatore quantistico.
Il parametro shot indica il numero di volto in cui si deve eseguire l’esperimento: di solito sul simulatore si fanno 100 cicli, mentre sul computer quantistico almeno 1000. Il massimo è 8192 esecuzioni del codice, ma si può anche provare ad eseguire una sola volta il codice tanto per vedere se funziona.
Infine, si può semplicemente avviare l’esperimento con il metodo run_experiment delle API. Il risultato viene fornito sotto forma di array, e ciò che ci interessa è l’elemento status.
Di fatto, quindi, eseguire un esperimento è molto semplice, bastano poche righe di codice con le quali si controllano tutti i parametri dell’esperimento e si può leggere il risultato. Python è quindi una ottima opzione per eseguire esperimenti in modo automatizzato. Se si è alle prime armi, tuttavia, conviene utilizzare l’interfaccia web del sito ufficiale per capire come muoversi nella scrittura del codice OpenQASM.
Programmare il calcolatore quantistico
Per imparare il linguaggio nativo del calcolatore quantistico di IBM si può leggere la guida ufficiale, pubblicata assieme ad alcuni esempi su GitHub. Ovviamente è in lingua inglese, ma si occupa di spiegare in modo schematico tutto quello che serve, se non per scrivere dei programmi, almeno per capire gli esempi. In particolare, a pagina 9 è presente una tabella con i principali comandi del linguaggio. Uno dei metodi migliori per utilizzare davvero il calcolatore quantistico di IBM è sfruttare le API per Python. I programmi “quantistici” non si scrivono in Python, si deve sempre usare il codice nativo OpenQASM, ma Python può essere un modo semplice per lanciare i programmi “quantistici” dal nostro computer.